Intervals, vibrations, and frequency ratios
The intervals we use in music are actually frequency ratios of the individual tones and they usually reflect frequency relationships between vibrations within the tones itself.
First, a short bit of sound theory
Tones are periodic waves, air molecules vibrating in a certain frequency. Usually, tones consist of vibrations in various frequencies that are multiples of the lowest, called the fundamental. These tones are said to have a harmonic spectrum. For example, a tone of 100 Hz — Hertz, i.e. 100 cycles per second — may include vibrations of 200, 300, 400, 500, and 600 Hz, theoretically up to infinity. These individual vibrations are called harmonics, sometimes referred to as the combination of a fundamental frequency and its overtones. Mathematically, every periodic wave can be split into a collection of sine waves1.
The amplitude relationships between the harmonics of a tone, define the timbre or spectrum. Such tones can be generated by wind instruments, string instruments, or by sound synthesis. Due to the physics of a string, its overtones are slightly out of tune (quasi-harmonic). This effect grows as the string gets thicker and shorter, but for the purpose of this article, we don’t need to take this into account. Furthermore, as a rule of thumb, one can say: the higher the overtone, the lower its amplitude.
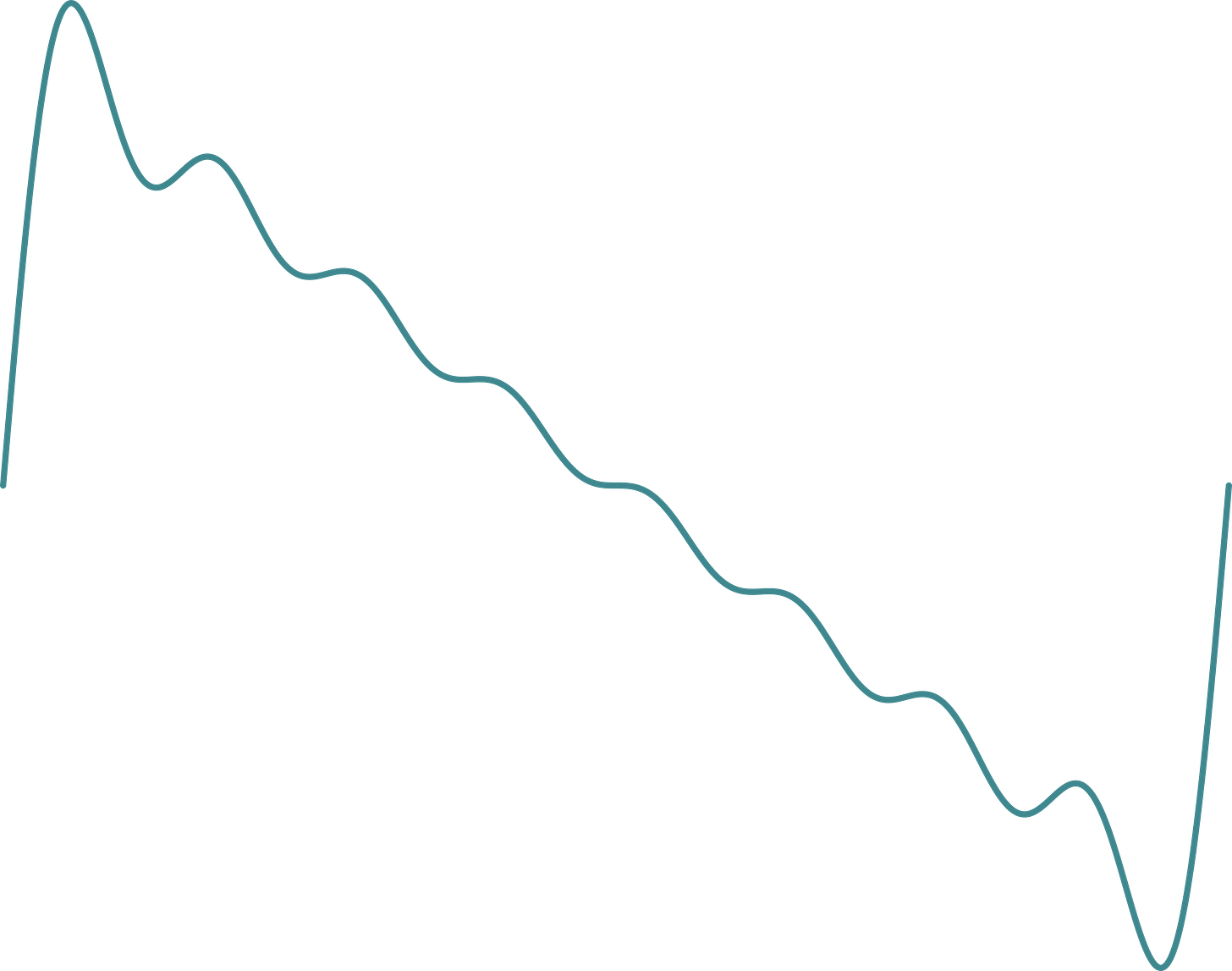
A typical waveform is a sawtooth wave, as shown below as one period of the fundamental. It’s a sum of sine waves with the same phase, while the amplitude of every partial — yet another word for harmonic — is divided by its frequency ratio to the fundamental. They are artificial (synthesized) waveforms, this one limited to eight partials. Adding partials according to the described procedure, will make the waveform sharpen, until it will end up being just a straight diagonal line.
The image above is actually a graph of the following function. One can determine immediately how to add more harmonics.
Intervals and harmonics
Tonal systems, like the well-known diatonic scale, are usually based on the relationships between harmonics. These relationships are integer relationships, since they’re based on whole numbers. What we call an octave, is actually a frequency ratio of 1:2 between two tones. The term octave, or eighth note, is used since the diatonic scale puts seven notes between a doubling of the frequency, so intervals smaller than an octave, have a smaller ratio than 1:2. A fifth for example resembles 2:3, a major third 4:5. This is why some intervals sound more consonant than others, because many of their harmonics overlap and tones blend in perfectly. I will publish an in-depth article on this subject — consonancy and how scales are created — in the near future.
The frequency of a vibrating string
Roughly, there are three main parameters that define the frequency, also called pitch, of a vibrating string: tension, length, and thickness. The thickness is usually fixed, defined while stringing the instrument. The tension can then be adjusted by tuners before playing, to arrive at the required pitch. String lengths for individual strings are already defined at the stage of designing the instrument, but some instruments — like a violin or a guitar— are built for adjusting the string lengths by the player. They put a finger on the string to make it shorter. Guitarists, especially on electric guitars, also bend strings to increase tension and thus pitch. Guitars usually feature frets on their fingerboards to easily switch between notes within a collection of fixed pitches.
String length and frequency relationships
The simple formula is that dividing the string length by a certain value, will multiply the frequency by that same value. So, dividing the string length by two, results in double the frequency. The fret to play the octave is therefore placed at the middle of the string, the double octave (sixteenth) on 3/4 of the string, leaving only one quarter of the string to vibrate, thus four times the frequency of the open string. The equation to calcalute the fret distance D from the bridge (thus the vibrating part), where S is the string length, and r is the frequency ratio:
However, we usually want to know the fret distance from the nut rather than the bridge, so if we redefine D as distance from the nut, we just need to take the string length and subtract the distance from the bridge. This results in:
A perfect fifth with frequency ratio 3:22, would therefore need a fret at 1/3rd of of the string length, in order to have 2/3rd of the string vibrate. Considering a string length — in terms of a guitar also called scale length — of 24 inches, the fret would need to be placed eight inches from the nut.
Regular 12-TET
Fast-forward to a regular modern guitar…
The most common approach for tuning instruments for the diatonic scale for the last two centuries, is by just dividing the octave in twelve equal steps. Since we’re talking frequency ratios here, these are steps on a logarithmic scale. Why this happened, other options, and my personal approach in for example the meantone guitar, will be discussed in-depth in future articles (i.e. music and tuning theory classes) here.
The formula for calculating these steps, where r is the frequency ratio and n is the number of steps — also called semitones — is:
Now, we only need to combine the last two simple equations to find the distances from the nut for any fret n in the 12-TET system.
Good luck!
This is called Fourier analysis, named after Joseph Fourier. Fourier analysis on wikipedia
Since we need the fifth above and not below the open string pitch, I turned around the ratio used previously, thus 3/2 is the number we need instead of 2/3.